Implement Your First Artificial Neuron From Scratch
Last Updated on November 14, 2021 by Editorial Team
Author(s): Satya Ganesh
Understand, Implement, and visualize an Artificial Neuron from scratch using python.
Introduction
Warren McCulloch and Walter Pitts first proposed artificial neurons in the year 1943, and it is a highly simplified computational model which resembles its behavior with neurons possessed by the human brain. Before we dig deeper into the concepts of artificial neurons let us take a look at the biological neuron.
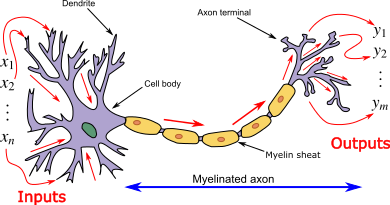
Biological Neuron
The biological neuron receives input signals through dendrites and sends them to the soma or cell body which is the processing unit of a neuron, the processed signal is then carried through the axon to other neurons. The junction where two neurons meet is called a synapse, the degree of synapse tells the strength of signal carried to other neurons.
Artificial Neuron — McCulloch Pitts Neuron (MP Neuron)
McCulloch Pitts Neuron model is also called a Threshold Logic Unit (TLU), or Linear Threshold Unit, it is named so because the output value of the neuron depends on a threshold value. The working of a biological neuron inspires this artificial neuron, it is structured and meant to behave similarly to biological neurons.
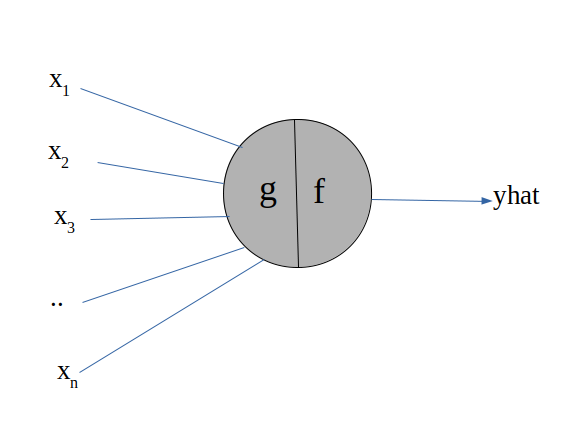
Input Vector [x₁ x₂ x₃…xₙ] — In an Artificial neuron, the input vector act as inputs to the neuron, it behaves similar to dendrites in Biological Neuron.
Function f(x) — In an Artificial neuron, the function f(x) is a summation function, which behaves similar to soma in Biological neurons.
A. Model of MP Neuron
We can define the Model as an approximation function, of the true relationship between the dependent and independent variables.
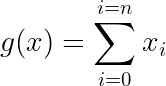
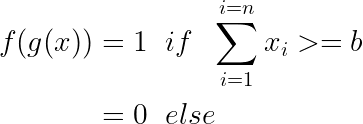
[x₁ x₂ x₃ … xₙ] — inputs or attributes of the MP Neuron Model.
b — Threshold Values which is the only parameter in the MP Neuron Model.
The function g(x) performs a summation of all the inputs and the function f(x) applies a threshold value to the output returned by the function g(x). The value returned by the function f(x) is a boolean value, that is, if the summation of inputs is greater than the fixed threshold(b) then the neuron gets activated else the neuron is fired.
Things you need to know about MP Neuron
- It takes only binary data, which is input vector X ϵ {0,1}.
- Task performed by the neuron is binary classification ie Y ϵ {0,1}.
Geometrical Interpretation of MP Neuron
For simplicity let us consider there are only two features in the dataset, so the input vector looks like, x = [x₁ x₂], and the functions look like…
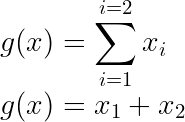
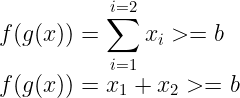
converting it into the form of linear equation ie, y = m*x + c
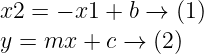
compare equations(1) and (2), we find that…
The slope of the line m = -1 (it is fixed for any dataset).
The y-intercept of the line c= b (the only thing we can change to tune the model).
Note: all the points that lie on top of the line are classified as positive(1) and all the points that lie below the line are classified as negative(0).
when we plot the line x2 = -x1 + 1
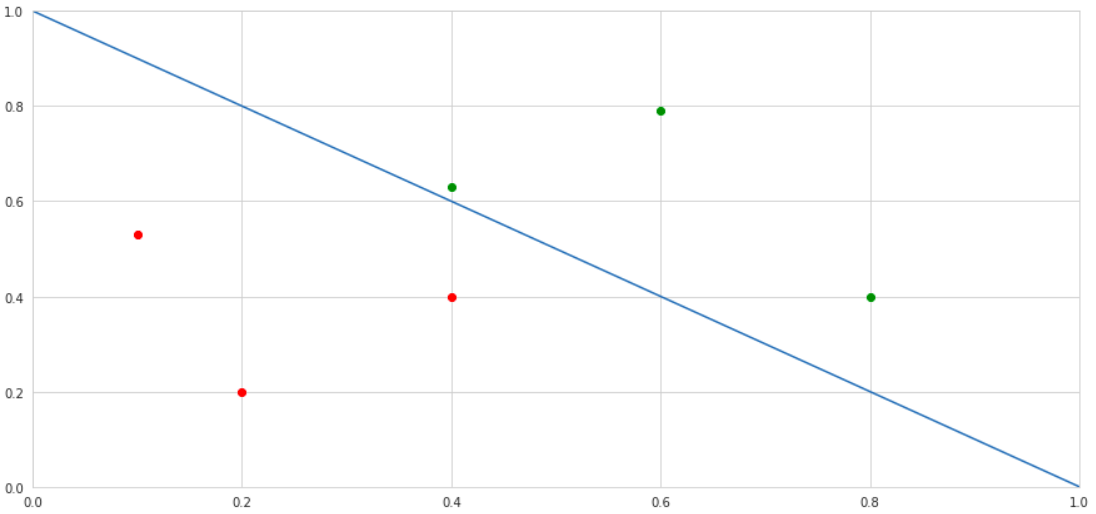
Summary :
- All the points above the line (green points) are classified as positive.
- All the points below the line (red points) are classified as negative.
- MP Neuron model works only when the points are linearly separable.
- The slope of the line in the MP Neuron model is fixed that is -1.
- We have got the power to change the value of y-intercept(b).
B. Loss function
Loss is the error or mistake that the model has incurred during its training phase, it can be calculated using the mean squared error loss function.
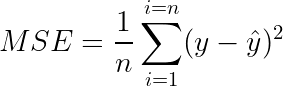
C. Optimization Algorithm
since the only parameter in the model is b, we need to choose the best value of b such that the loss is reduced.
We can choose the b value using a brute force approach since the range of b is from [0,n], where n is the number of features in data.
- b takes a minimum value when x₁ + x₂ + x₃ … xₙ =0, ie when feature vector looks like [x₁ x₂ x₃ … xₙ]= [0 0 0 …0]
- b takes a maximum value when x₁ + x₂ + x₃ … xₙ =n, ie when feature vector looks like [x₁ x₂ x₃ … xₙ] = [1 1 1 … 1]
since the value of b lies between [0,n], we can compute loss the model incurred for each value of b and pick the best one among them.
D. Evaluation
we can evaluate the performance of the model using this simple formula
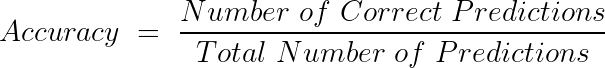
E. Limitation of MP Neuron Model
- The Model accepts data only in the form of {0,1}, we can not feed it with real values.
- It is only used for Binary classification.
- It performs well only when data is linearly separable
- The line equation has a fixed slope, so there is no flexibility in changing the slope of the line.
- We can not judge which feature is more important and we can not give priority to any feature.
- The learning algorithm is not so impressive, we are using a brute force approach to find the threshold value.
Let’s Code…

Data Requirements
we use the breast cancer dataset present in the sklearn datasets package, and our task is to predict if the person has cancer or not based on the data provided
A. Importing essential libraries
B. Loading Data
C. Visualizing Data
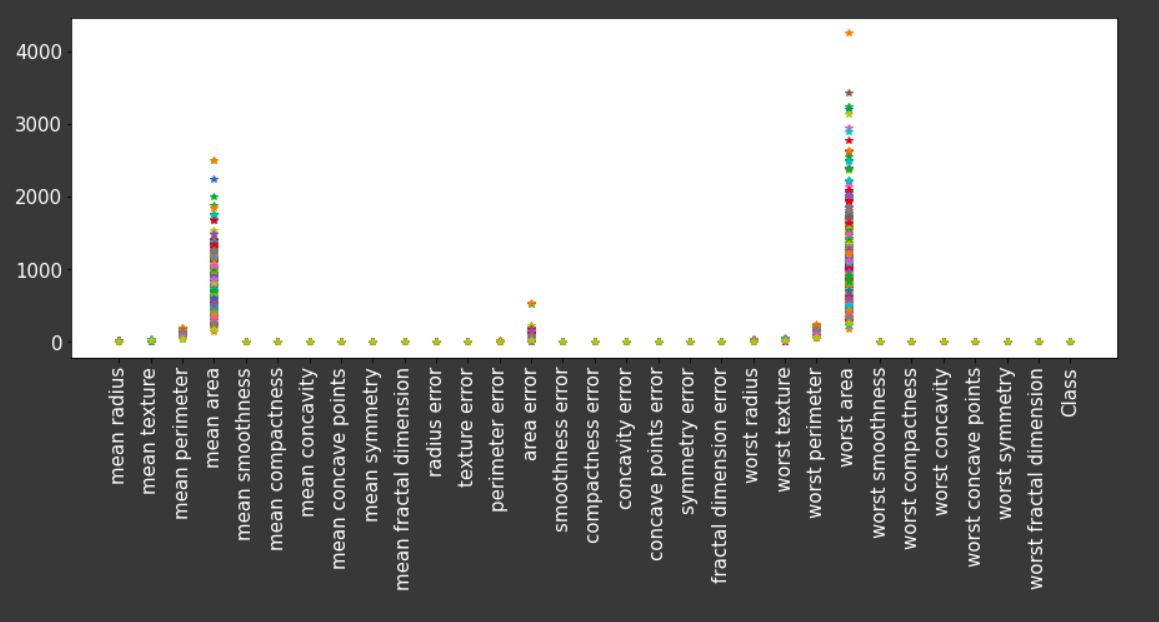
From the above plot, we infer that data is not in binary form but for the MP neuron model requires we require data to be in binary form that is {0,1}. So let’s convert this data into binary form. before that, we need to split the data into train data and test data
D. Splitting Data into train and test data
E. Binning data
Here we convert the data into zeros and ones, to make it compatible with the MP Neuron model, we do this using the cut method in the pandas library.

F. Defining the MP Neuron
G. Evaluation

on the training data the performance of the model is pretty good, ie 84.6%, let visualize the performance of the model for different values of b.
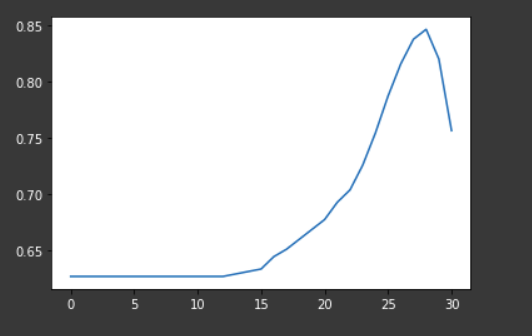
performance on test data

Conclusion
We build a very simplified computational model of a biological neuron, and we got 78% accuracy on test data that is not bad for such a simple model. I hope you learned something new from this article.
References
- Wikipedia
- NPTEL course on Deep Learning

 Logo:
Logo:  Areas Served:
Areas Served: